POST
浅谈数字签名
近日,腾讯公司状告贵州老干妈的新闻在互联网上闹得沸沸扬扬,💥 大家也应该有所耳闻。腾讯起诉老干妈合作推广后没有付广告费,但随后老干妈否认了此事,称完全不知道这个合作。 😕 后来经调查发现,这是三个人冒充老干妈市场部经理,然后刻了个假公章,就为了获得合作后的游戏礼包并从中牟利。
且不说这个事情的性质,就从三个骗子用一个假公章,居然把腾讯骗得团团转来看,也折射出来目前的一些问题。
试想如果腾讯在和老干妈的合同中使用了数字签名… 上述事件根本就不会发生。
这篇文章就来聊一聊数字签名。文章比较长,心急的读者可以选择直接跳到相关章节阅读。
本文就从散列函数开始说起,然后引出 👉 数字摘要技术和非对称加密技术,最后介绍基于这两个技术应用的数字签名。
1. 数字摘要技术
1.1 散列函数
官方解释:散列函数一般是指Hash函数,是一种从任何一种数据中创建小的数字指纹的方法。散列函数把消息或数据压缩成摘要,使得数据量变小,将数据的格式固定下来。
我的理解:散列函数是将任意长度的消息映射成为定长的散列值的函数,以该散列值(消息摘要)作为认证符。
1.2 密码散列函数
密码散列函数(Cryptographic hash function),又译为加密散列函数,是散列函数的一种。这种散列函数的输入数据,通常被称为消息(message),而它的输出结果,经常被称为消息摘要(message digest)或摘要(digest)。将任意长度的消息压缩到某一固定长度的消息摘要,一个理想的密码散列函数应该有四个主要的特性:
- 对于任何一个给定的消息,它都很容易就能运算出散列数值(摘要)。
- 难以由一个已知的散列数值 (摘要),去推算出原始的消息。(评注:单向,不可逆)
- 在不更动散列数值 (摘要) 的前提下,修改消息内容是不可行的。(评注:唯一性)
- 对于两个不同的消息,它不能给与相同的散列数值 (摘要)。
单向散列函数生成的信息摘要是不可预见的,消息摘要看起来和原始的数据没有任何的关系。而且,原始数据的任何微小变化都会对生成的信息摘要产生很大的影响。
1.3 MD5
MD5信息摘要算法(MD5, Message-Digest Algorithm),一种被广泛使用的密码散列函数,可以产生出一个128位(16字节)的散列值(hash value),用于确保信息传输完整一致。
应用:
- 用于密码管理 - 把用户的密码以MD5值(或类似的其它算法)的方式保存起来,用户注册的时候,系统是把用户输入的密码计算成 MD5 值,然后再去和系统中保存的 MD5 值进行比较,如果密文相同,就可以认定密码是正确的,否则密码错误。通过这样的步骤,系统在并不知道用户密码明码的情况下就可以确定用户登录系统的合法性。
- 电子签名 - 使用 MD5算法就可以为任何文件(不管其大小、格式、数量)产生一个独一无二的
数字指纹,借助这个数字指纹,通过检查文件前后 MD5 值是否发生了改变,就可以知道源文件是否被改动。
1.4 SHA
安全散列算法(SHA, Secure Hash Algorithm)是一个密码散列函数家族,是FIPS所认证的安全散列算法。SHA家族的五个算法,分别是SHA-1、SHA-224、SHA-256、SHA-384,和SHA-512,后四者有时并称为SHA-2。SHA在许多安全协定中广为使用,包括TLS和SSL、PGP、SSH、S/MIME和IPsec,曾被视为是MD5(更早之前被广为使用的杂凑函数)的后继者。
1.5 HMAC
HMAC是密钥相关的哈希运算消息认证码(Hash-based Message Authentication Code)的缩写,它可以与任何迭代散列函数捆绑使用。HMAC算法是一种基于密钥的报文完整性的验证方法 ,其安全性是建立在Hash加密算法基础上的。它要求通信双方共享密钥、约定算法、对报文进行Hash运算,形成固定长度的认证码。通信双方通过认证码的校验来确定报文的合法性。 HMAC算法可以用来作加密、数字签名、报文验证等。
HMAC是一种利用密码学中的散列函数来进行消息认证的一种机制,所能提供的消息认证包括两方面内容:
- ① 消息完整性认证:能够证明消息内容在传送过程没有被修改。
- ② 信源身份认证:因为通信双方共享了认证的密钥,接收方能够认证发送该数据的信源与所宣称的一致,即能够可靠地确认接收的消息与发送的一致。
1.6 消息认证码
消息认证(message authentication)就是验证消息的完整性,当接收方收到发送方的报文时,接收方能够验证收到的报文是真实的和未被篡改的。
消息认证所用的摘要算法与一般的对称或非对称加密算法不同,它并不用于防止信息被窃取,而是用于证明原文的完整性和准确性,也就是说,消息认证主要用于防止信息被篡改。
消息认证码(Message authentication code,缩写为MAC)又译为消息鉴别码、文件消息认证码、讯息鉴别码、信息认证码,是经过特定算法后产生的一小段信息,检查某段消息的完整性,以及作身份验证。
它可以用来:
- 检查消息的完整性
- 鉴别消息的来源
消息认证码的算法中,通常会使用带密钥的散列函数(HMAC),或者块密码的带认证工作模式(如CBC-MAC)。信息鉴别码不能提供对信息的保密,若要同时实现保密认证,同时需要对信息进行加密。
以上为数字摘要技术的内容,接下来我们讲一讲非对称加密技术。
2. 非对称加密技术
非对称加密算法需要两个密钥:公开密钥(public key:简称pk)和私有密钥(Secret key:简称sk)。公钥与私钥是一对,如果用公钥对数据进行加密,只有用对应的私钥才能解密。
非对称加密算法实现机密信息交换的基本过程是:甲方生成一对密钥并将公钥公开,需要向甲方发送信息的其他角色(乙方)使用该密钥(甲方的公钥)对机密信息进行加密后再发送给甲方;甲方再用自己私钥对加密后的信息进行解密。甲方想要回复乙方时正好相反,使用乙方的公钥对数据进行加密,同理,乙方使用自己的私钥来进行解密。另一方面,甲方可以使用自己的私钥对机密信息进行签名后再发送给乙方;乙方再用甲方的公钥对甲方发送回来的数据进行验签。
2.1 RSA
RSA是一种公钥密码算法,被用于公钥密码和数字签名。RSA是一种非对称加密技术。
RSA密钥至少为500位长,一般推荐使用1024位。这就使加密的计算量很大。为减少计算量,在传送信息时,常采用传统加密方法与公开密钥加密方法相结合的方式,即信息采用改进的DES或IDEA对话密钥加密,然后使用RSA密钥加密对话密钥和信息摘要。对方收到信息后,用不同的密钥解密并可核对信息摘要。
RSA算法的保密强度随其密钥的长度增加而增强。但是,密钥越长,其加解密所耗用的时间也越长。速度一直是RSA的缺陷。一般来说只用于少量数据加密。RSA的速度比对应同样安全级别的对称密码算法要慢很多。
通过上面的介绍,我们可以总结出RSA的特性:
既可以用公钥加密然后私钥解密,也可以用私钥加密然后公钥解密
- 公钥加密然后私钥解密,可以用于通信中拥有公钥的一方向拥有私钥的另一方传递机密信息,不被第三方窃听。可应用在原文的加密。
- 那么私钥加密然后公钥解密是用在什么场合呢?就是数字签名(摘要的加密)。
3. 数字签名
数字签名(又称公钥数字签名)是只有信息的发送者才能产生的别人无法伪造的一段数字串,这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。
通过发送数字签名,
接收者可以
- 确认接收到的消息(报文)的完整性,发送过程中有没有被篡改
- 鉴别发送者的身份
- 防抵赖
发送者可以
- 加密信息
- 防止伪造信息
- 防止重放攻击
数字签名应用非对称密钥加密技术与数字摘要技术。
数字签名技术是将摘要信息用发送者的私钥加密,与原文一起传送给接收者。接收者用自己的公钥解密被加密的摘要信息,然后用HASH函数对收到的原文产生一个摘要信息,与解密的摘要信息对比。如果相同,则说明收到的信息是完整的,在传输过程中没有被修改,否则说明信息被修改过,因此数字签名能够验证信息的完整性。数字签名是个加密的过程,数字签名验证是个解密的过程。
如果签名者想要对某个文件进行数字签名,公钥必须向CA (身份认证机构)来注册。注册后身份认证机构给你发一数字证书。对文件签名后,你把此数字证书连同文件及签名一起发给接受者,接受者向身份认证机构求证是否真地是用你的密钥签发的文件。
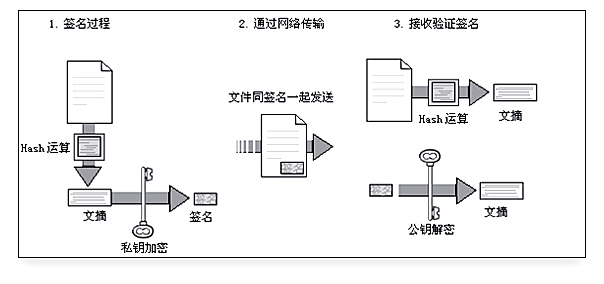
3.1 签名过程
- 在正式的数字签名中,发送方首先对发送文件采用哈希算法,得到一个固定长度的消息摘要(Message Digest);
- 再用自己的私钥(Secret key,SK)对消息摘要进行签名,形成发送方的数字签名。
- 数字签名将作为队件和原文一起发送给接收方;
- 接收方首先用发送方的公钥对数字签名进行解密得到发送方的数字摘要,然后用相同的哈希函数对原文进行哈希计算,得到一个新的消息摘要,最后将消息摘要与收到的消息摘要做比较。
3.1.1 例子
一个完整的签名例子如下。
为了保证信息传送的保密性、真实性、完整性和不可否认性,需要对传送的信息进行数字加密和签名,其传送过程为:
- 发送者准备好要传送的数字信息(明文)
- 发送者对数字信息进行哈希运算(SH256/MD5),得到一个信息摘要;
- 发送者用自己的私钥对信息摘要进行加密得到数字签名(RSA),并将其附在数字信息上;
- 发送者随机产生一个加密密钥,并用此密码对要发送的信息(明文)进行加密(对称加密DES),形成密文;
- 发送者用接收者的公钥对刚才随机产生的加密密钥🔑进行加密,将加密后的
DES密钥连同密文一起传送给接收者;- 接收者收到传送来的密文和加密过的DES密钥,先用自己的私钥对加密的DES密钥进行解密,得到发送者随机产生的加密密钥;
- 接收者然后用随机密钥🔑对收到的密文进行解密,得到明文的数字信息,然后将随机密钥抛弃;
- 接收者用发送者的公钥对发送者的数字签名进行解密,得到信息摘要;
- 接收者用相同的哈希算法对收到的明文再进行一次哈希运算,得到一个新的信息摘要;
- 接收者将收到的信息摘要和新产生的信息摘要进行比较,如果一致,说明收到的信息没有被修改过,并且确实来自于发送者。
3.2 X.509
最后我们来说一下数字签名中用于公钥的数字证书,为了证明公钥的有效性和合法性,信息发送者必须向CA (身份认证机构)来注册。注册后身份认证机构给你发一数字证书。信息发送者在签名时必须将数字证书连同文件及签名一起发给接受者,接受者接收到信息后会通过数字证书确认是否手里的公钥为发送者的。
X.509正是一种数字证书的格式标准。
3.2.1 格式
X.509规定了数字证书的格式。
大致如下:
版本号
序列号
签名算法
颁发者
证书有效期
开始日期
终止日期
主题
主题公钥信息
公钥算法
主体公钥
颁发者唯一身份信息(可选)
主题唯一身份信息(可选)
扩展信息(可选)
签名3.2.2 扩展名
X.509有多种常用的扩展名。不过其中的一些还用于其它用途,就是说具有这个扩展名的文件可能并不是证书,比如说可能只是保存了私钥。
| 扩展名 | 说明 |
|---|---|
| .pem(隐私增强型电子邮件) | DER编码的证书再进行Base64编码的数据存放在-----BEGIN CERTIFICATE-----和-----END CERTIFICATE-----之中 |
| .cer/.crt/.der | 通常是DER二进制格式的,但Base64编码后也很常见。 |
| p7b/.p7c | PKCS |
| .p12 | PKCS#12格式,包含证书的同时可能还有带密码保护的私钥。 |
| .pfx | PKCS#12之前的格式(通常用PKCS#12格式,比如那些由IIS产生的PFX文件)。 |
3.3 SSL证书
符合X.509格式的证书有多种,这里以SSL证书为例。
常见的场景会是下面这样:
- 客户端,比如浏览器会向服务端发送请求,服务端为了证明自己的身份,会发送证书给对方。
- 浏览器读取证书的数字签名部分,用自身根证书列表中对应的公钥证书对其进行解密。如果解密成功,并且证书哈希值与签名内的哈希值匹配一致,可证明站点提供的证书确实是该CA根证书签发的,否则给出风险提示。
- 验证通过之后,使用证书中的公钥对随机数和对称加密算法加密,发送给服务端,服务端用私钥进行解密,获得密钥和加密算法。
- 服务端与浏览器后续通信将会使用新的对称加密算法和随机密钥加密信息。
SSL证书从生成到使用涉及到了三次加解密过程:
- 证书生成的时候利用私钥签名,验证证书的时候利用公钥解密。
- 确认证书有效后,利用证书中的公钥进行加密,服务端利用私钥解密。
- 双方使用新生成的随机密钥进行数据加解密。
用一张结构图表示下HTTPS和X.509的关系:
HTTPS
/ \
HTTP TLS/SSL
/ \
通信内容 确认身份
对称加密 SSL证书 —— X.509 格式,非对称加密3.4 数字签名应用
- 网站认证
最常见的用处就是用来认证一个网站的身份,用浏览器打开任何一个网站,然后点击地址栏前面的 🔒,点击查看证书,就可以看到网站的数字签名证书了。看过之前的内容我们就知道数字证书其实是对公钥的封装,在公钥的基础上添加了诸如颁发者之类的信息。
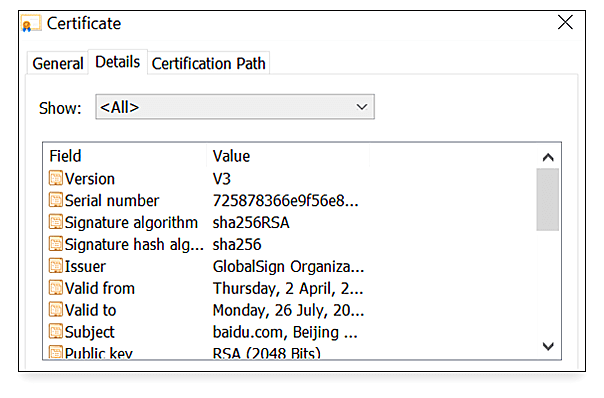
签名算法一栏可以看到,它使用的是sha256RSA,也就是使用SHA-256计算摘要,然后使用RSA对摘要进行签名。
-
代码签名
而除此之外,还有个地方我们经常碰到数字签名的——代码签名。
代码签名用于确保其来源可靠且未被篡改。 -
比特币
比特币是一种完全匿名的数字货币,它的身份认证是基于ECDSA。比特币的账户地址就是对公钥计算摘要得到的,向全世界公布。而确认你是账户拥有者的唯一办法就是看你有没有账户对应的私钥。对于比特币中的任意一个交易记录,只有当其中付款方的签名是有效的,它才是有效的。
3.5 生成数字签名
在Windows平台下,Microsoft提供了一组工具用于生成和校验数字签名。关于这部分内容,我会另外写一篇文章介绍如何利用 Microsoft WDK 工具来生成数字签名。
最后推荐一篇文章,讲的比我好,如果看了以上内容还有不明白的地方,可以继续阅读这篇文章。