POST
电容式触摸检测技术原理
智能手机的兴起不仅仅是由于操作系统上的改变,更多的是由于引入了一种新的人机交互的模式。这种全新的模式导致了用户体验的大幅度改善。电容式触摸检测技术正是其中的关键技术。
电容式触摸检测本质上是一种精密的电信号测量技术,其测量的电荷变化量为皮库伦级别。触控IC通过高精度的ADC采样触摸屏上的电压信号,在人手或者其他导电体接触到设备后,检测到的电压信号会发生变化(mv级别),这些变化量被采样到触控IC内部,从而可以被识别到。
而这其中又涉及到触摸屏ITO的工艺制造和图案的设计,不同的ITO叠层和图案的设计都会对触控检测产生影响。
ITO全称是纳米铟锡金属氧化物,主要有这两点特性,透明和导电。适合应用于在屏幕上贴合透明的导电层的需求。
目前常见的ITO叠层分为双层(搭桥/不搭桥)和单层方案,按照基材来看的话有PET和Glass的选择,按照贴合方式的话分为全贴合和框贴的方式。 具体可以演化为 GFF(PFF)/OGS(G1/G2)/GG/GF 等,由于不同的叠层设计导致工艺的难度和良率不同,生产出的触摸屏厚度也不一样,因此大多数手机ODM都会根据不同的ID设计要求和造价来进行评估。在触控的性能方面,一般来说双层ITO由于出线的方式和Cm(X/Y 耦合电容)控制方面的优势,性能上比较容易把握。早期的单层方案适合做单点触控(比如应用三角形图案),目前也有单层多点的方案,但是由于单层出线,在减小bonding pad面积和走线Gap方面都面临一些挑战。
目前也有面板厂商主推的On-Cell/In-Cell 方案,将ITO嵌入到显示面板内部,减少了整体的厚度。现在看来是未来的发展方向,但是技术难度大,良率的控制是一个问题,目前仍有许多的挑战。
ITO的图形常见的有菱形/三角形/长条形/毛毛虫形等。以及基于菱形的一些变形图案,比如雪花形等。其中菱形/长条形应用于两层ITO的设计,三角形应用于单层单点的触控,毛毛虫的图案用于单层多点的开发。性能方面也有不同,比如菱形的方案由于电场的分布一致性好,因此在触摸检测的精度和线性度方面有优势,另外变形的方案,比如雪花形,是在菱形的方案上增加了X,Y层的耦合面积,因此在灵敏度方面更好,另外对于一些小面积的物体,比如1mm的passive stylus的检测精度上有提升。
本文主要是对触控IC检测原理的说明,因此以上关于触摸屏设计方面的内容不会占用太多的篇幅描述,我会另外写一篇博客来展开详细的讨论。
检测原理
我们现在以下面的图片作为开始
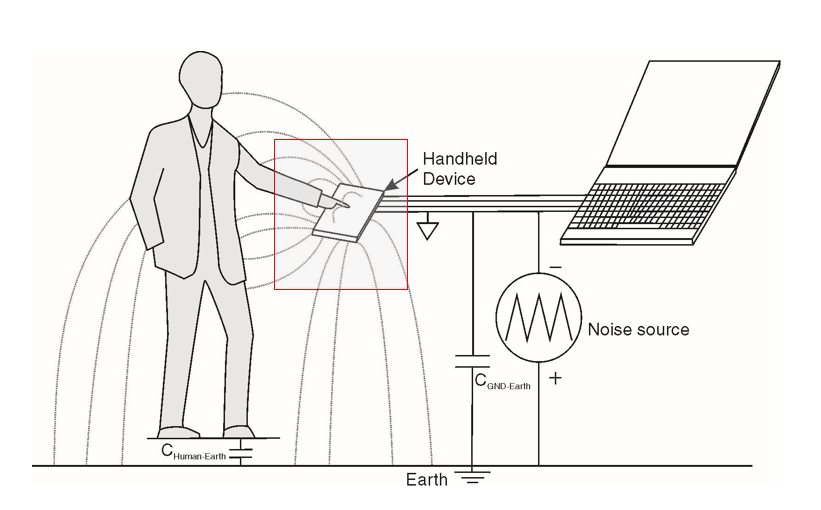
电路模型
这张图片代表了一个人机操作的模型,其中手持设备的信号地通过一个耦合电容Cgnd-earth与大地相连。我们将重点放到手持设备上。细化一下模型,如下图。
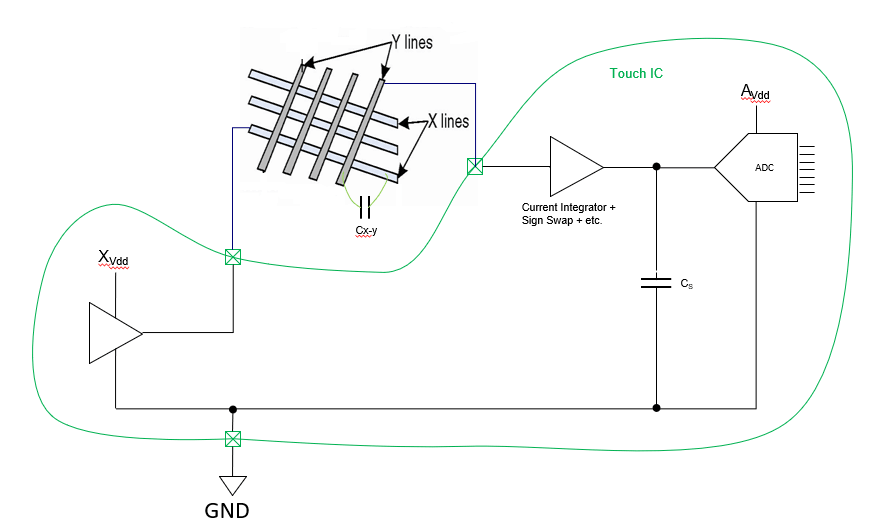
这是一个完整触摸设备的模型,其中X,Y 分别是触摸屏的ITO 走线X和Y, Cx-y为x和y之间的耦合电容,通常也叫互电容Cm。X线作为信号驱动线连接到触控IC的TX输出端,Y线作为接收线连接到触控IC的输入端口,该端口的信号会被送入IC内部的ADC采样。在ADC的输入端与IC的信号地之间有一个采样电容 Cs 用于积累电荷,在ADC的采样端形成电压信号。注意此图片所示是没有人手触摸的情形下的模型。
我们继续简化一下模型,将它转化为电路的形式。
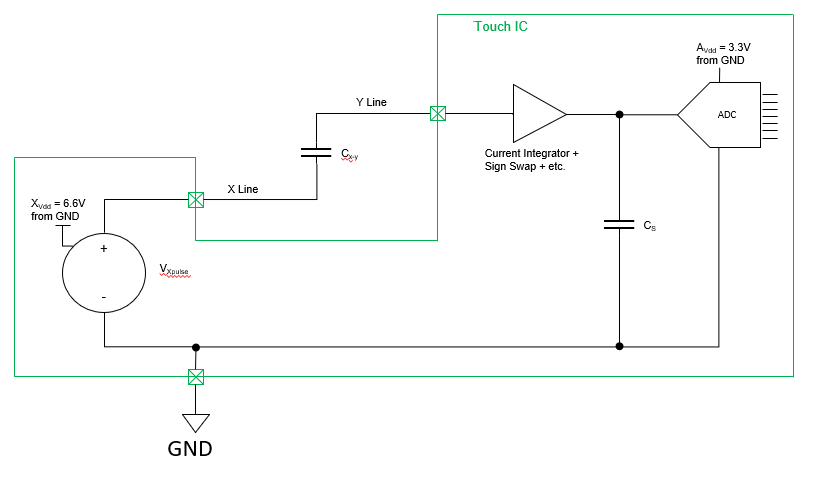
从以上图就比较清晰了,从IC 信号源正端输出的电荷流经Cx-y和Cs,并最终通过GND 回到信号源的负端。这期间会在Cx-y和Cm两端建立起电压。
我们来对整个过程做一个计算,假设信号源输出的电压为6.6V,Cxy为2pF,Cs为18pF,电流积分电路静态时可以视为短路。ADC 为10位转换,参考电压3.3v。
根据公式
Q = C × ΔV (Qtotal = Csystem × ΔV)
可以计算出系统中的总电荷量为
Csystem = 1/(1/Cx-y + 1/Cs) = 1/(1/2pF + 1/18pF) = 1.8pF
Qtotal = 1.8pF × 6.6V = 11.88pC
其中在Cs两侧的建立的电压为
ΔVacross Cs = Q / Cs = 11.88pC / 18pF = 0.66V。
这个电压会被ADC采样从而得到一个ADC的数值给到IC做计算
0.66V / 3.3V × 1024 = 205 ADC counts
至此我们做一个总结。
| 电荷 | Cs 电压 | ADC 值 |
|---|---|---|
| 11.88pc | 0.66v | 205 |
下面我们对有手指触摸的情况做一个分析。
手指触摸时的模型如下图
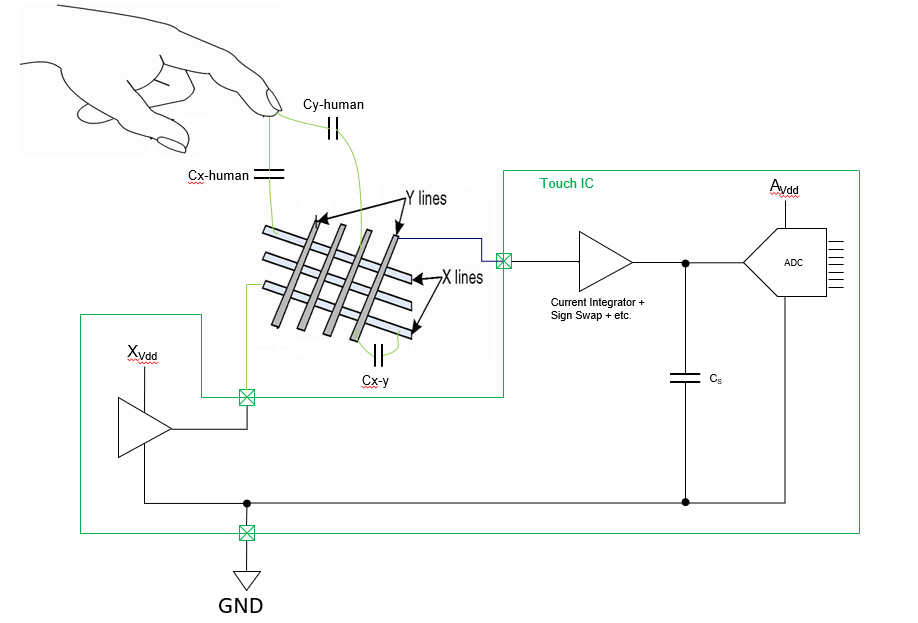
由于人体本身是导体,因此在手接触到触摸屏表面后会导入Cx-human和Cy-human两个耦合电容。这就给之前讲到的电荷流经的途径中增加了一个通路,即一部分电荷通过人体流经大地回流到设备信号源。同刚才的例子一样,我们进一步简化模型以电路的形式呈现。
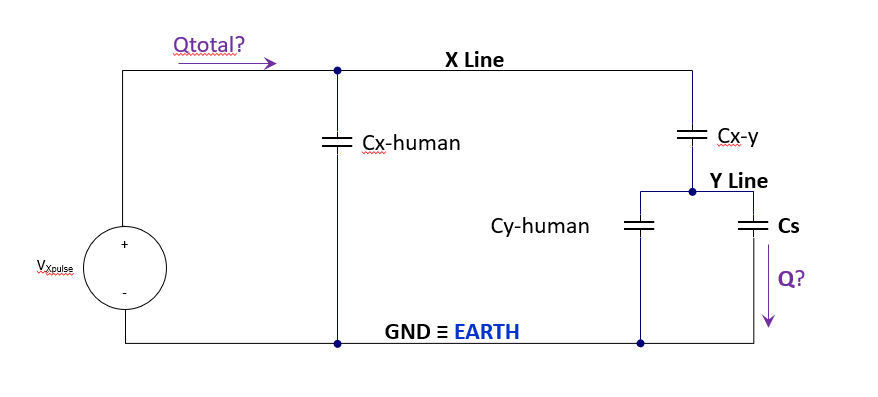
我们依旧继续刚才的计算,假设Cy-human = 2pF, Cx-human = 2pF, Cx-y = 2pF and Cs = 18pF. 则流程系统的总电荷为
Ca = Cy-human + Cs = 2pF + 18pF = 20pF
Cb = 1 / (1/Cx-y + 1/Ca) = 1 / (1/2pF + 1/20pF) = 1.81pF
Csystem = Cx-human + Cb = 2pF + 1.81pF = 3.81pF
Qtotal = Csystem × ΔV = 3.81pF × 6.6V = 25.2pC
我们可以计算出电路中电荷的分布如下
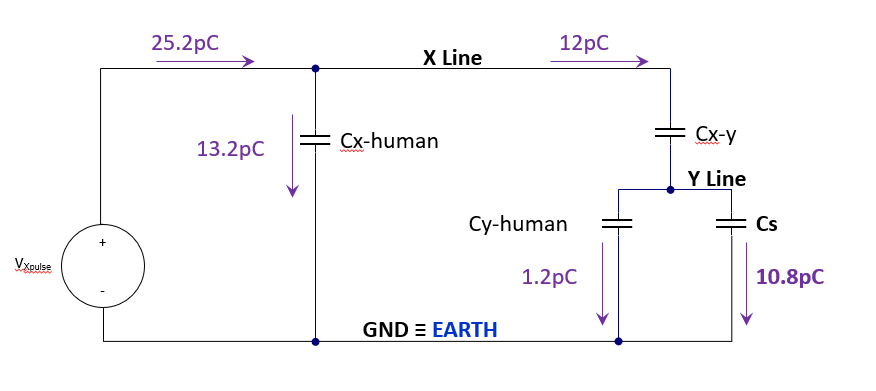
因此可以得出Cs两端的电压
ΔVacross Cs = Q / Cs = 10.8pC / 18pF = 0.6V
而ADC的数值为 0.6V / 3.3V × 1024 = 186 ADC counts
我们把手指触摸时的数据填入刚才的表格,
| 电荷 | Cs 电压 | ADC 值 |
|---|---|---|
| 11.88pc | 0.66v | 205 |
| 10.8pc | 0.6v | 186 |
我们得出不同情形下两次ADC采样的差值 205-186 = 19
通过两次采样时的ADC差值,触控IC 就可以检测到触摸屏上电压的变化,从而感知到人手触摸的动作。当然以上只是一个简单的模型和处理,用于描述触摸技术的检测原理,实际的应用中会对检测到的信号做很多处理,比如放大,过采样技术,双边沿积分等手段来放大差异,增加信号的robust和可识别性等。以上会涉及到IC厂家的专利保密技术,不在本文的讨论范围内。